4 ключа
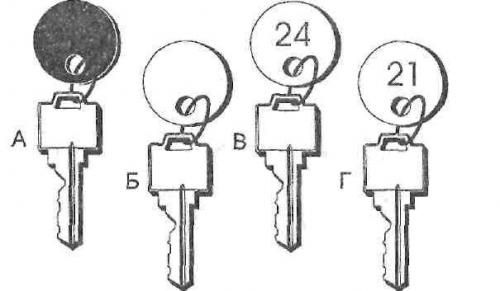
Одна сторона брелка либо черного, либо белого цвета, а на другой стороне указан либо четный, либо нечетный номер. Взгляните на 4 ключа на рисунке. Какие 2 из них вы возьмете, чтобы посмотреть на другую сторону брелка и узнать: верно ли, что все ключи с черными брелками имеют нечетные номера?
Ответ на загадку
Источник: Энциклопедия Головоломок
Автор перевода книги с анг.языка: Капышина Н.
Acula
21.01.2011 - 18:57
Всё хорошо, но если бы был виден рисунок, загадку можно было бы ещё и поотгадывать
Acula
22.01.2011 - 21:11
Ключи А и В. Если окажется на обратной стороне А нечётный номер, а обратная сторона В — белая, значит, утверждение верное.
афонька
27.01.2011 - 08:13
Акула, ты не прав(а)!!!!!!!!! Возьмем А и Г
роксана
01.02.2011 - 17:53
да возьмем а и г
Acula
08.02.2011 - 15:45
Вы абсолютно правы — я невнимательно номер писала хD
Конечно же, надо смотреть на обратные стороны черного и нечетного (раз про них вопрос)… а мне меньше в облаках витать
Acula
11.02.2011 - 00:34
Не, стоп. Вы меня запутали! Всё правильно я первый раз написала!
полина
18.02.2011 - 17:53
а и в
Дашуля
24.02.2011 - 10:29
так не думаю девки это задача тупая какаето
Karra
10.03.2011 - 11:06
A и Г, потомучто надо доказать что обязательно «если черный брелок, то число нечетное».
Б — не нужно, потомучто брелок белый и все равно какой номер с друго стороны.
В — не нужно, потомучто число четное и нас не интересует его цвет.
🙂
Антон
13.03.2011 - 10:13
Чо за фигню в ответе написали?
Если А нечетный, то брелок В — белый, а Г либо белый, либо черный…
Какое то тупое умозаключение…
Мышь
13.10.2011 - 01:32
Что-то я логики в ответе не увидела. Может, кто иначе пояснит?
Даже если все ключи с черными брелками имеют нечетные номера, это еще не доказывает, что все ключи с белыми брелками имеют четные номера. В условиях это не указано. Зачем смотреть на ключ с четным номером?
Мышь
13.10.2011 - 01:37
Все. Дошло. Действительно, ответ А и В. Г может оказаться черным, но это не докажет, что остальные черные брелки всегда с нечетными числами. А если В черный, то утверждение «черный=нечетный» автоматически становится неверным.
Мышь
13.10.2011 - 02:03
А вообще возникает вопрос, достаточно ли двух совпадений, чтоб принять их за закономерность?
Ромагн
24.03.2012 - 20:52
Надо перевернуть 1й и 3й.
1й — чтоб узнать четный или нет, а 3й, чтоб узнать вторую часть вопроса (все ли?)
2й нас не интересует, так как белый, а 4й не интересен, так как если он белый, то понятно почему не интересует, а если черный, то автоматом подходит к утверждению.