Прогулка с собакой

Месье и мадам Дюбуа пошли прогуляться со своей собакой. Каждый из них хотел сам держать поводок. Поэтому в конце концов они прицепили к ошейнику бедного животного два поводка, по 1 м длины каждый. Предположим, месье и мадам Дюбуа идут все время на расстоянии 1 м друг от друга.
Чему равна в каждый момент времени площадь участка, по которому может свободно бегать собака?
Ответ на загадку:
Пусть О и О’ — точки, в которых в некоторой заданный момент времени находятся месье и мадам Дюбуа. Если бы собаку держал на поводке только месье Дюбуа, то площадь участка равнялась бы я (площади круга радиусом 1 м). Точно так же обстояло бы дело и в случае, если бы собаку держала одна мадам Дюбуа.
Однако на самом деле участок, по которому может передвигаться собака, совпадает с пересечением этих двух кругов радиусом 1 м, центры которых удалены друг от друга на 1 м. Пусть А и В — точки пересечения соответствующих окружностей (с центрами О и О’ и радиусами 1 м).

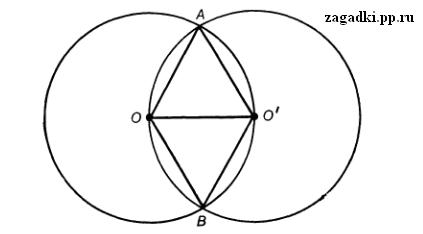
Тогда площадь ромба ОАО’В равна
2(площадь ОАО’)=3^1/2/2.
Площадь сектора с центром О, ограниченного точками Л и В, равна пи/3 и площадь сектора с центром О’, ограниченного точками А и В, равна пи/3. Следовательно, площадь пересечения наших двух кругов равна
пи/3+пи/3 — 3^1/2/2. =1,228.